Great dodecahedron

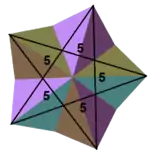
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.

Great dodecahedron
TypeKepler–Poinsot polyhedron
Stellation coreregular dodecahedron
ElementsF = 12, E = 30
V = 12 (χ = -6)
Faces by sides12{5}
Schläfli symbol{5,5⁄2}
Face configurationV(5⁄2)5
Wythoff symbol5⁄2 | 2 5
Coxeter diagram
Symmetry groupIh, H3, [5,3], (*532)
ReferencesU35, C44, W21
PropertiesRegular nonconvex

(55)/2
(Vertex figure)
Small stellated dodecahedron
(dual polyhedron)
3D model of a great dodecahedron

The discovery of the great dodecahedron is sometimes credited to Louis Poinsot in 1810, though there is a drawing of something very similar to a great dodecahedron in the 1568 book Perspectiva Corporum Regularium by Wenzel Jamnitzer.

The great dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the (n – 1)-pentagonal polytope faces of the core n-polytope (pentagons for the great dodecahedron, and line segments for the pentagram) until the figure again closes.

Images
Transparent model Spherical tiling

(With animation)
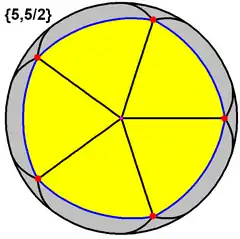This polyhedron represents a spherical tiling with a density of 3. (One spherical pentagon face is shown above in yellow)
Net Stellation
× 20
Net for surface geometry; twenty isosceles triangular pyramids, arranged like the faces of an icosahedron
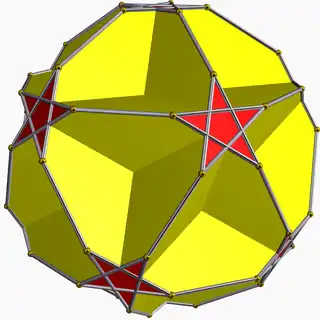
It can also be constructed as the second of three stellations of the dodecahedron, and referenced as Wenninger model [W21].
Animated truncation sequence from {5/2, 5} to {5, 5/2}

It shares the same edge arrangement as the convex regular icosahedron; the compound with both is the small complex icosidodecahedron.

If only the visible surface is considered, it has the same topology as a triakis icosahedron with concave pyramids rather than convex ones. The excavated dodecahedron can be seen as the same process applied to a regular dodecahedron, although this result is not regular.

A truncation process applied to the great dodecahedron produces a series of nonconvex uniform polyhedra. Truncating edges down to points produces the dodecadodecahedron as a rectified great dodecahedron. The process completes as a birectification, reducing the original faces down to points, and producing the small stellated dodecahedron.

Stellations of the dodecahedron
Platonic solid Kepler–Poinsot solids
Dodecahedron Small stellated dodecahedron Great dodecahedron Great stellated dodecahedron
Name Small stellated dodecahedron Dodecadodecahedron Truncated
great
dodecahedron		 Great
dodecahedron
Coxeter-Dynkin
diagram
Picture

Usage

See also

References
    • Baez, John "Golay code," Visual Insight, December 1, 2015.
  • Weisstein, Eric W., "Great dodecahedron" ("Uniform polyhedron") at MathWorld.
  • Weisstein, Eric W. "Three dodecahedron stellations". MathWorld.
  • Uniform polyhedra and duals
  • Metal sculpture of Great Dodecahedron
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.