How do I search for a number in a 2d array sorted left to right and top to bottom?

Question

I was recently given this interview question and I'm curious what a good solution to it would be.

Say I'm given a 2d array where all the numbers in the array are in increasing order from left to right and top to bottom.

What is the best way to search and determine if a target number is in the array?

Now, my first inclination is to utilize a binary search since my data is sorted. I can determine if a number is in a single row in O(log N) time. However, it is the 2 directions that throw me off.

Another solution I thought may work is to start somewhere in the middle. If the middle value is less than my target, then I can be sure it is in the left square portion of the matrix from the middle. I then move diagonally and check again, reducing the size of the square that the target could potentially be in until I have honed in on the target number.

Does anyone have any good ideas on solving this problem?

Example array:

Sorted left to right, top to bottom.

1  2  4  5  6  
2  3  5  7  8  
4  6  8  9  10  
5  8  9  10 11  

Answer 1

Here's a simple approach:

1. Start at the bottom-left corner.
2. If the target is less than that value, it must be above us, so move up one.
3. Otherwise we know that the target can't be in that column, so move right one.
4. Goto 2.

For an NxM array, this runs in O(N+M). I think it would be difficult to do better. :)

---

Edit: Lots of good discussion. I was talking about the general case above; clearly, if N or M are small, you could use a binary search approach to do this in something approaching logarithmic time.

Here are some details, for those who are curious:

History

This simple algorithm is called a Saddleback Search. It's been around for a while, and it is optimal when N == M. Some references:

• David Gries, The Science of Programming. Springer-Verlag, 1989.
• Edsgar Dijkstra, The Saddleback Search. Note EWD-934, 1985.

However, when N < M, intuition suggests that binary search should be able to do better than O(N+M): For example, when N == 1, a pure binary search will run in logarithmic rather than linear time.

Worst-case bound

Richard Bird examined this intuition that binary search could improve the Saddleback algorithm in a 2006 paper:

• Richard S. Bird, Improving Saddleback Search: A Lesson in Algorithm Design, in Mathematics of Program Construction, pp. 82--89, volume 4014, 2006.

Using a rather unusual conversational technique, Bird shows us that for N <= M, this problem has a lower bound of Ω(N * log(M/N)). This bound make sense, as it gives us linear performance when N == M and logarithmic performance when N == 1.

Algorithms for rectangular arrays

One approach that uses a row-by-row binary search looks like this:

1. Start with a rectangular array where N < M. Let's say N is rows and M is columns.
2. Do a binary search on the middle row for value. If we find it, we're done.
3. Otherwise we've found an adjacent pair of numbers s and g, where s < value < g.
4. The rectangle of numbers above and to the left of s is less than value, so we can eliminate it.
5. The rectangle below and to the right of g is greater than value, so we can eliminate it.
6. Go to step (2) for each of the two remaining rectangles.

In terms of worst-case complexity, this algorithm does log(M) work to eliminate half the possible solutions, and then recursively calls itself twice on two smaller problems. We do have to repeat a smaller version of that log(M) work for every row, but if the number of rows is small compared to the number of columns, then being able to eliminate all of those columns in logarithmic time starts to become worthwhile.

This gives the algorithm a complexity of T(N,M) = log(M) + 2 * T(M/2, N/2), which Bird shows to be O(N * log(M/N)).

Another approach posted by Craig Gidney describes an algorithm similar the approach above: it examines a row at a time using a step size of M/N. His analysis shows that this results in O(N * log(M/N)) performance as well.

Performance Comparison

Big-O analysis is all well and good, but how well do these approaches work in practice? The chart below examines four algorithms for increasingly "square" arrays:

(The "naive" algorithm simply searches every element of the array. The "recursive" algorithm is described above. The "hybrid" algorithm is an implementation of Gidney's algorithm. For each array size, performance was measured by timing each algorithm over fixed set of 1,000,000 randomly-generated arrays.)

Some notable points:

• As expected, the "binary search" algorithms offer the best performance on rectangular arrays and the Saddleback algorithm works the best on square arrays.
• The Saddleback algorithm performs worse than the "naive" algorithm for 1-d arrays, presumably because it does multiple comparisons on each item.
• The performance hit that the "binary search" algorithms take on square arrays is presumably due to the overhead of running repeated binary searches.

Summary

Clever use of binary search can provide O(N * log(M/N) performance for both rectangular and square arrays. The O(N + M) "saddleback" algorithm is much simpler, but suffers from performance degradation as arrays become increasingly rectangular.

Answer 2

This problem takes Θ(b lg(t)) time, where b = min(w,h) and t=b/max(w,h). I discuss the solution in this blog post.

Lower bound

An adversary can force an algorithm to make Ω(b lg(t)) queries, by restricting itself to the main diagonal:

Legend: white cells are smaller items, gray cells are larger items, yellow cells are smaller-or-equal items and orange cells are larger-or-equal items. The adversary forces the solution to be whichever yellow or orange cell the algorithm queries last.

Notice that there are b independent sorted lists of size t, requiring Ω(b lg(t)) queries to completely eliminate.

Algorithm

1. (Assume without loss of generality that w >= h)
2. Compare the target item against the cell t to the left of the top right corner of the valid area
   • If the cell's item matches, return the current position.
   • If the cell's item is less than the target item, eliminate the remaining t cells in the row with a binary search. If a matching item is found while doing this, return with its position.
   • Otherwise the cell's item is more than the target item, eliminating t short columns.
3. If there's no valid area left, return failure
4. Goto step 2

Finding an item:

Determining an item doesn't exist:

Legend: white cells are smaller items, gray cells are larger items, and the green cell is an equal item.

Analysis

There are b*t short columns to eliminate. There are b long rows to eliminate. Eliminating a long row costs O(lg(t)) time. Eliminating t short columns costs O(1) time.

In the worst case we'll have to eliminate every column and every row, taking time O(lg(t)*b + b*t*1/t) = O(b lg(t)).

Note that I'm assuming lg clamps to a result above 1 (i.e. lg(x) = log_2(max(2,x))). That's why when w=h, meaning t=1, we get the expected bound of O(b lg(1)) = O(b) = O(w+h).

Code

public static Tuple<int, int> TryFindItemInSortedMatrix<T>(this IReadOnlyList<IReadOnlyList<T>> grid, T item, IComparer<T> comparer = null) {
    if (grid == null) throw new ArgumentNullException("grid");
    comparer = comparer ?? Comparer<T>.Default;

    // check size
    var width = grid.Count;
    if (width == 0) return null;
    var height = grid[0].Count;
    if (height < width) {
        var result = grid.LazyTranspose().TryFindItemInSortedMatrix(item, comparer);
        if (result == null) return null;
        return Tuple.Create(result.Item2, result.Item1);
    }

    // search
    var minCol = 0;
    var maxRow = height - 1;
    var t = height / width;
    while (minCol < width && maxRow >= 0) {
        // query the item in the minimum column, t above the maximum row
        var luckyRow = Math.Max(maxRow - t, 0);
        var cmpItemVsLucky = comparer.Compare(item, grid[minCol][luckyRow]);
        if (cmpItemVsLucky == 0) return Tuple.Create(minCol, luckyRow);

        // did we eliminate t rows from the bottom?
        if (cmpItemVsLucky < 0) {
            maxRow = luckyRow - 1;
            continue;
        }

        // we eliminated most of the current minimum column
        // spend lg(t) time eliminating rest of column
        var minRowInCol = luckyRow + 1;
        var maxRowInCol = maxRow;
        while (minRowInCol <= maxRowInCol) {
            var mid = minRowInCol + (maxRowInCol - minRowInCol + 1) / 2;
            var cmpItemVsMid = comparer.Compare(item, grid[minCol][mid]);
            if (cmpItemVsMid == 0) return Tuple.Create(minCol, mid);
            if (cmpItemVsMid > 0) {
                minRowInCol = mid + 1;
            } else {
                maxRowInCol = mid - 1;
                maxRow = mid - 1;
            }
        }

        minCol += 1;
    }

    return null;
}

Answer 3

I would use the divide-and-conquer strategy for this problem, similar to what you suggested, but the details are a bit different.

This will be a recursive search on subranges of the matrix.

At each step, pick an element in the middle of the range. If the value found is what you are seeking, then you're done.

Otherwise, if the value found is less than the value that you are seeking, then you know that it is not in the quadrant above and to the left of your current position. So recursively search the two subranges: everything (exclusively) below the current position, and everything (exclusively) to the right that is at or above the current position.

Otherwise, (the value found is greater than the value that you are seeking) you know that it is not in the quadrant below and to the right of your current position. So recursively search the two subranges: everything (exclusively) to the left of the current position, and everything (exclusively) above the current position that is on the current column or a column to the right.

And ba-da-bing, you found it.

Note that each recursive call only deals with the current subrange only, not (for example) ALL rows above the current position. Just those in the current subrange.

Here's some pseudocode for you:

bool numberSearch(int[][] arr, int value, int minX, int maxX, int minY, int maxY)

if (minX == maxX and minY == maxY and arr[minX,minY] != value)
    return false
if (arr[minX,minY] > value) return false;  // Early exits if the value can't be in 
if (arr[maxX,maxY] < value) return false;  // this subrange at all.
int nextX = (minX + maxX) / 2
int nextY = (minY + maxY) / 2
if (arr[nextX,nextY] == value)
{
    print nextX,nextY
    return true
}
else if (arr[nextX,nextY] < value)
{
    if (numberSearch(arr, value, minX, maxX, nextY + 1, maxY))
        return true
    return numberSearch(arr, value, nextX + 1, maxX, minY, nextY)
}
else
{
    if (numberSearch(arr, value, minX, nextX - 1, minY, maxY))
        return true
    reutrn numberSearch(arr, value, nextX, maxX, minY, nextY)
}

Answer 4

The two main answers give so far seem to be the arguably O(log N) "ZigZag method" and the O(N+M) Binary Search method. I thought I'd do some testing comparing the two methods with some various setups. Here are the details:

The array is N x N square in every test, with N varying from 125 to 8000 (the largest my JVM heap could handle). For each array size, I picked a random place in the array to put a single 2. I then put a 3 everywhere possible (to the right and below of the 2) and then filled the rest of the array with 1. Some of the earlier commenters seemed to think this type of setup would yield worst case run time for both algorithms. For each array size, I picked 100 different random locations for the 2 (search target) and ran the test. I recorded avg run time and worst case run time for each algorithm. Because it was happening too fast to get good ms readings in Java, and because I don't trust Java's nanoTime(), I repeated each test 1000 times just to add a uniform bias factor to all the times. Here are the results:

ZigZag beat binary in every test for both avg and worst case times, however, they are all within an order of magnitude of each other more or less.

Here is the Java code:

public class SearchSortedArray2D {

    static boolean findZigZag(int[][] a, int t) {
        int i = 0;
        int j = a.length - 1;
        while (i <= a.length - 1 && j >= 0) {
            if (a[i][j] == t) return true;
            else if (a[i][j] < t) i++;
            else j--;
        }
        return false;
    }

    static boolean findBinarySearch(int[][] a, int t) {
        return findBinarySearch(a, t, 0, 0, a.length - 1, a.length - 1);
    }

    static boolean findBinarySearch(int[][] a, int t,
            int r1, int c1, int r2, int c2) {
        if (r1 > r2 || c1 > c2) return false; 
        if (r1 == r2 && c1 == c2 && a[r1][c1] != t) return false;
        if (a[r1][c1] > t) return false;
        if (a[r2][c2] < t) return false;

        int rm = (r1 + r2) / 2;
        int cm = (c1 + c2) / 2;
        if (a[rm][cm] == t) return true;
        else if (a[rm][cm] > t) {
            boolean b1 = findBinarySearch(a, t, r1, c1, r2, cm - 1);
            boolean b2 = findBinarySearch(a, t, r1, cm, rm - 1, c2);
            return (b1 || b2);
        } else {
            boolean b1 = findBinarySearch(a, t, r1, cm + 1, rm, c2);
            boolean b2 = findBinarySearch(a, t, rm + 1, c1, r2, c2);
            return (b1 || b2);
        }
    }

    static void randomizeArray(int[][] a, int N) {
        int ri = (int) (Math.random() * N);
        int rj = (int) (Math.random() * N);
        a[ri][rj] = 2;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (i == ri && j == rj) continue;
                else if (i > ri || j > rj) a[i][j] = 3;
                else a[i][j] = 1;
            }
        }
    }

    public static void main(String[] args) {

        int N = 8000;
        int[][] a = new int[N][N];
        int randoms = 100;
        int repeats = 1000;

        long start, end, duration;
        long zigMin = Integer.MAX_VALUE, zigMax = Integer.MIN_VALUE;
        long binMin = Integer.MAX_VALUE, binMax = Integer.MIN_VALUE;
        long zigSum = 0, zigAvg;
        long binSum = 0, binAvg;

        for (int k = 0; k < randoms; k++) {
            randomizeArray(a, N);

            start = System.currentTimeMillis();
            for (int i = 0; i < repeats; i++) findZigZag(a, 2);
            end = System.currentTimeMillis();
            duration = end - start;
            zigSum += duration;
            zigMin = Math.min(zigMin, duration);
            zigMax = Math.max(zigMax, duration);

            start = System.currentTimeMillis();
            for (int i = 0; i < repeats; i++) findBinarySearch(a, 2);
            end = System.currentTimeMillis();
            duration = end - start;
            binSum += duration;
            binMin = Math.min(binMin, duration);
            binMax = Math.max(binMax, duration);
        }
        zigAvg = zigSum / randoms;
        binAvg = binSum / randoms;

        System.out.println(findZigZag(a, 2) ?
                "Found via zigzag method. " : "ERROR. ");
        //System.out.println("min search time: " + zigMin + "ms");
        System.out.println("max search time: " + zigMax + "ms");
        System.out.println("avg search time: " + zigAvg + "ms");

        System.out.println();

        System.out.println(findBinarySearch(a, 2) ?
                "Found via binary search method. " : "ERROR. ");
        //System.out.println("min search time: " + binMin + "ms");
        System.out.println("max search time: " + binMax + "ms");
        System.out.println("avg search time: " + binAvg + "ms");
    }
}

Answer 5

This is a short proof of the lower bound on the problem.

You cannot do it better than linear time (in terms of array dimensions, not the number of elements). In the array below, each of the elements marked as * can be either 5 or 6 (independently of other ones). So if your target value is 6 (or 5) the algorithm needs to examine all of them.

1 2 3 4 *
2 3 4 * 7
3 4 * 7 8
4 * 7 8 9
* 7 8 9 10

Of course this expands to bigger arrays as well. This means that this answer is optimal.

Update: As pointed out by Jeffrey L Whitledge, it is only optimal as the asymptotic lower bound on running time vs input data size (treated as a single variable). Running time treated as two-variable function on both array dimensions can be improved.

Answer 6

I think Here is the answer and it works for any kind of sorted matrix

bool findNum(int arr[][ARR_MAX],int xmin, int xmax, int ymin,int ymax,int key)
{
    if (xmin > xmax || ymin > ymax || xmax < xmin || ymax < ymin) return false;
    if ((xmin == xmax) && (ymin == ymax) && (arr[xmin][ymin] != key)) return false;
    if (arr[xmin][ymin] > key || arr[xmax][ymax] < key) return false;
    if (arr[xmin][ymin] == key || arr[xmax][ymax] == key) return true;

    int xnew = (xmin + xmax)/2;
    int ynew = (ymin + ymax)/2;

    if (arr[xnew][ynew] == key) return true;
    if (arr[xnew][ynew] < key)
    {
        if (findNum(arr,xnew+1,xmax,ymin,ymax,key))
            return true;
        return (findNum(arr,xmin,xmax,ynew+1,ymax,key));
    } else {
        if (findNum(arr,xmin,xnew-1,ymin,ymax,key))
            return true;
        return (findNum(arr,xmin,xmax,ymin,ynew-1,key));
    }
}

Answer 7

Interesting question. Consider this idea - create one boundary where all the numbers are greater than your target and another where all the numbers are less than your target. If anything is left in between the two, that's your target.

If I'm looking for 3 in your example, I read across the first row until I hit 4, then look for the smallest adjacent number (including diagonals) greater than 3:

1 2 4 5 6
2 3 5 7 8
4 6 8 9 10
5 8 9 10 11

Now I do the same for those numbers less than 3:

1 2 4 5 6
2 3 5 7 8
4 6 8 9 10
5 8 9 10 11

Now I ask, is anything inside the two boundaries? If yes, it must be 3. If no, then there is no 3. Sort of indirect since I don't actually find the number, I just deduce that it must be there. This has the added bonus of counting ALL the 3's.

I tried this on some examples and it seems to work OK.

Answer 8

Binary search through the diagonal of the array is the best option. We can find out whether the element is less than or equal to the elements in the diagonal.

Answer 9

I've been asking this question in interviews for the better part of a decade and I think there's only been one person who has been able to come up with an optimal algorithm.

My solution has always been:

1. Binary search the middle diagonal, which is the diagonal running down and right, containing the item at (rows.count/2, columns.count/2).

2. If the target number is found, return true.

3. Otherwise, two numbers (u and v) will have been found such that u is smaller than the target, v is larger than the target, and v is one right and one down from u.

4. Recursively search the sub-matrix to the right of u and top of v and the one to the bottom of u and left of v.

I believe this is a strict improvement over the algorithm given by Nate here, since searching the diagonal often allows a reduction of over half the search space (if the matrix is close to square), whereas searching a row or column always results in an elimination of exactly half.

Here's the code in (probably not terribly Swifty) Swift:

import Cocoa

class Solution {
    func searchMatrix(_ matrix: [[Int]], _ target: Int) -> Bool {
        if (matrix.isEmpty || matrix[0].isEmpty) {
            return false
        }

        return _searchMatrix(matrix, 0..<matrix.count, 0..<matrix[0].count, target)
    }

    func _searchMatrix(_ matrix: [[Int]], _ rows: Range<Int>, _ columns: Range<Int>, _ target: Int) -> Bool {
        if (rows.count == 0 || columns.count == 0) {
            return false
        }
        if (rows.count == 1) {
            return _binarySearch(matrix, rows.lowerBound, columns, target, true)
        }
        if (columns.count == 1) {
            return _binarySearch(matrix, columns.lowerBound, rows, target, false)
        }

        var lowerInflection = (-1, -1)
        var upperInflection = (Int.max, Int.max)
        var currentRows = rows
        var currentColumns = columns
        while (currentRows.count > 0 && currentColumns.count > 0 && upperInflection.0 > lowerInflection.0+1) {
            let rowMidpoint = (currentRows.upperBound + currentRows.lowerBound) / 2
            let columnMidpoint = (currentColumns.upperBound + currentColumns.lowerBound) / 2
            let value = matrix[rowMidpoint][columnMidpoint]
            if (value == target) {
                return true
            }

            if (value > target) {
                upperInflection = (rowMidpoint, columnMidpoint)
                currentRows = currentRows.lowerBound..<rowMidpoint
                currentColumns = currentColumns.lowerBound..<columnMidpoint
            } else {
                lowerInflection = (rowMidpoint, columnMidpoint)
                currentRows = rowMidpoint+1..<currentRows.upperBound
                currentColumns = columnMidpoint+1..<currentColumns.upperBound
            }
        }
        if (lowerInflection.0 == -1) {
            lowerInflection = (upperInflection.0-1, upperInflection.1-1)
        } else if (upperInflection.0 == Int.max) {
            upperInflection = (lowerInflection.0+1, lowerInflection.1+1)
        }

        return _searchMatrix(matrix, rows.lowerBound..<lowerInflection.0+1, upperInflection.1..<columns.upperBound, target) || _searchMatrix(matrix, upperInflection.0..<rows.upperBound, columns.lowerBound..<lowerInflection.1+1, target)
    }

    func _binarySearch(_ matrix: [[Int]], _ rowOrColumn: Int, _ range: Range<Int>, _ target: Int, _ searchRow : Bool) -> Bool {
        if (range.isEmpty) {
            return false
        }

        let midpoint = (range.upperBound + range.lowerBound) / 2
        let value = (searchRow ? matrix[rowOrColumn][midpoint] : matrix[midpoint][rowOrColumn])
        if (value == target) {
            return true
        }

        if (value > target) {
            return _binarySearch(matrix, rowOrColumn, range.lowerBound..<midpoint, target, searchRow)
        } else {
            return _binarySearch(matrix, rowOrColumn, midpoint+1..<range.upperBound, target, searchRow)
        }
    }
}

Answer 10

public boolean searchSortedMatrix(int arr[][] , int key , int minX , int maxX , int minY , int maxY){

    // base case for recursion
    if(minX > maxX || minY > maxY)
        return false ;
    // early fails
    // array not properly intialized
    if(arr==null || arr.length==0)
        return false ;
    // arr[0][0]> key return false
    if(arr[minX][minY]>key)
        return false ;
    // arr[maxX][maxY]<key return false
    if(arr[maxX][maxY]<key)
        return false ;
    //int temp1 = minX ;
    //int temp2 = minY ;
    int midX = (minX+maxX)/2 ;
    //if(temp1==midX){midX+=1 ;}
    int midY = (minY+maxY)/2 ;
    //if(temp2==midY){midY+=1 ;}


    // arr[midX][midY] = key ? then value found
    if(arr[midX][midY] == key)
        return true ;
    // alas ! i have to keep looking

    // arr[midX][midY] < key ? search right quad and bottom matrix ;
    if(arr[midX][midY] < key){
        if( searchSortedMatrix(arr ,key , minX,maxX , midY+1 , maxY))
            return true ;
        // search bottom half of matrix
        if( searchSortedMatrix(arr ,key , midX+1,maxX , minY , maxY))
            return true ;
    }
    // arr[midX][midY] > key ? search left quad matrix ;
    else {
         return(searchSortedMatrix(arr , key , minX,midX-1,minY,midY-1));
    }
    return false ;

}

Answer 11

The optimal solution is to start at the top-left corner, that has minimal value. Move diagonally downwards to the right until you hit an element whose value >= value of the given element. If the element's value is equal to that of the given element, return found as true.

Otherwise, from here we can proceed in two ways.

Strategy 1:

1. Move up in the column and search for the given element until we reach the end. If found, return found as true
2. Move left in the row and search for the given element until we reach the end. If found, return found as true
3. return found as false

Strategy 2: Let i denote the row index and j denote the column index of the diagonal element we have stopped at. (Here, we have i = j, BTW). Let k = 1.

• Repeat the below steps until i-k >= 0
  1. Search if a[i-k][j] is equal to the given element. if yes, return found as true.
  2. Search if a[i][j-k] is equal to the given element. if yes, return found as true.
  3. Increment k

1 2 4 5 6
2 3 5 7 8
4 6 8 9 10
5 8 9 10 11

Answer 12

A. Do a binary search on those lines where the target number might be on.

B. Make it a graph : Look for the number by taking always the smallest unvisited neighbour node and backtracking when a too big number is found

Answer 13

Binary search would be the best approach, imo. Starting at 1/2 x, 1/2 y will cut it in half. IE a 5x5 square would be something like x == 2 / y == 3 . I rounded one value down and one value up to better zone in on the direction of the targeted value.

For clarity the next iteration would give you something like x == 1 / y == 2 OR x == 3 / y == 5

Answer 14

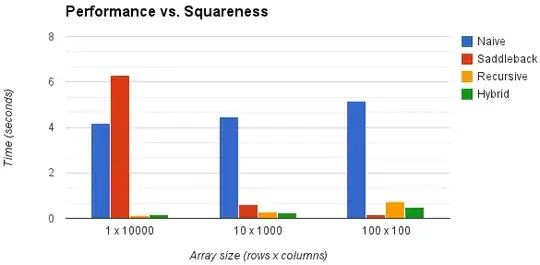
Well, to begin with, let us assume we are using a square.

1 2 3
2 3 4
3 4 5

1. Searching a square

I would use a binary search on the diagonal. The goal is the locate the smaller number that is not strictly lower than the target number.

Say I am looking for 4 for example, then I would end up locating 5 at (2,2).

Then, I am assured that if 4 is in the table, it is at a position either (x,2) or (2,x) with x in [0,2]. Well, that's just 2 binary searches.

The complexity is not daunting: O(log(N)) (3 binary searches on ranges of length N)

2. Searching a rectangle, naive approach

Of course, it gets a bit more complicated when N and M differ (with a rectangle), consider this degenerate case:

1  2  3  4  5  6  7  8
2  3  4  5  6  7  8  9
10 11 12 13 14 15 16 17

And let's say I am looking for 9... The diagonal approach is still good, but the definition of diagonal changes. Here my diagonal is [1, (5 or 6), 17]. Let's say I picked up [1,5,17], then I know that if 9 is in the table it is either in the subpart:

            5  6  7  8
            6  7  8  9
10 11 12 13 14 15 16

This gives us 2 rectangles:

5 6 7 8    10 11 12 13 14 15 16
6 7 8 9

So we can recurse! probably beginning by the one with less elements (though in this case it kills us).

I should point that if one of the dimensions is less than 3, we cannot apply the diagonal methods and must use a binary search. Here it would mean:

• Apply binary search on 10 11 12 13 14 15 16, not found
• Apply binary search on 5 6 7 8, not found
• Apply binary search on 6 7 8 9, not found

It's tricky because to get good performance you might want to differentiate between several cases, depending on the general shape....

3. Searching a rectangle, brutal approach

It would be much easier if we dealt with a square... so let's just square things up.

1  2  3  4  5  6  7  8
2  3  4  5  6  7  8  9
10 11 12 13 14 15 16 17
17 .  .  .  .  .  .  17
.                    .
.                    .
.                    .
17 .  .  .  .  .  .  17

We now have a square.

Of course, we will probably NOT actually create those rows, we could simply emulate them.

def get(x,y):
  if x < N and y < M: return table[x][y]
  else: return table[N-1][M-1]            # the max

so it behaves like a square without occupying more memory (at the cost of speed, probably, depending on cache... oh well :p)

Answer 15

EDIT:

I misunderstood the question. As the comments point out this only works in the more restricted case.

In a language like C that stores data in row-major order, simply treat it as a 1D array of size n * m and use a binary search.

Answer 16

I suggest, store all characters in a 2D list. then find index of required element if it exists in list.

If not present print appropriate message else print row and column as:

row = (index/total_columns) and column = (index%total_columns -1)

This will incur only the binary search time in a list.

Please suggest any corrections. :)

Answer 17

If O(M log(N)) solution is ok for an MxN array -

template <size_t n>
struct MN * get(int a[][n], int k, int M, int N){
  struct MN *result = new MN;
  result->m = -1;
  result->n = -1;

  /* Do a binary search on each row since rows (and columns too) are sorted. */
  for(int i = 0; i < M; i++){
    int lo = 0; int hi = N - 1;
    while(lo <= hi){
      int mid = lo + (hi-lo)/2;
      if(k < a[i][mid]) hi = mid - 1;
      else if (k > a[i][mid]) lo = mid + 1;
      else{
        result->m = i;
        result->n = mid;
        return result;
      }
    }
  }
  return result;
}

Working C++ demo.

Please do let me know if this wouldn't work or if there is a bug it it.

Answer 18

class Solution {
   public boolean searchMatrix(int[][] matrix, int target) {
    if(matrix == null)
        return false;
    int i=0;
    int j=0;
    int m = matrix.length;
    int n = matrix[0].length;
    boolean found = false;
    while(i<m && !found){
        while(j<n && !found){
            if(matrix[i][j] == target)
                found = true;
            if(matrix[i][j] < target)
                j++;
            else
                break;
        }
        i++;
        j=0;
    }
    return found; 
 }}

129 / 129 test cases passed.

Status: Accepted

Runtime: 39 ms

Memory Usage: 55 MB

Answer 19

I have a recursive Divide & Conquer Solution. Basic Idea for one step is: We know that the Left-Upper(LU) is smallest and the right-bottom(RB) is the largest no., so the given No(N) must: N>=LU and N<=RB

IF N==LU and N==RB::::Element Found and Abort returning the position/Index If N>=LU and N<=RB = FALSE, No is not there and abort. If N>=LU and N<=RB = TRUE, Divide the 2D array in 4 equal parts of 2D array each in logical manner.. And then apply the same algo step to all four sub-array.

My Algo is Correct I have implemented on my friends PC. Complexity: each 4 comparisons can b used to deduce the total no of elements to one-fourth at its worst case.. So My complexity comes to be 1 + 4 x lg(n) + 4 But really expected this to be working on O(n)

I think something is wrong somewhere in my calculation of Complexity, please correct if so..

Answer 20

Given a square matrix as follows:

[ a b c ]
[ d e f ]
[ i j k ]

We know that a < c, d < f, i < k. What we don't know is whether d < c or d > c, etc. We have guarantees only in 1-dimension.

Looking at the end elements (c,f,k), we can do a sort of filter: is N < c ? search() : next(). Thus, we have n iterations over the rows, with each row taking either O( log( n ) ) for binary search or O( 1 ) if filtered out.

Let me given an EXAMPLE where N = j,

1) Check row 1. j < c? (no, go next)

2) Check row 2. j < f? (yes, bin search gets nothing)

3) Check row 3. j < k? (yes, bin search finds it)

Try again with N = q,

1) Check row 1. q < c? (no, go next)

2) Check row 2. q < f? (no, go next)

3) Check row 3. q < k? (no, go next)

There is probably a better solution out there but this is easy to explain.. :)

Answer 21

As this is an interview question, it would seem to lead towards a discussion of Parallel programming and Map-reduce algorithms.

See http://code.google.com/intl/de/edu/parallel/mapreduce-tutorial.html