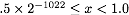What is the total number of unique values for a double in the range [0.0, 1.0)?

Question

Random.NextDouble() (a Double from the range [0.0,1.0)) is sometimes multiplied with a large Int64 (let Int64 big = 9000000000L), and the result floored to obtain a random Int64 value larger than what can be obtained from Random.Next() (an Int32 from the range [0,Int32.MaxValue)).

Random r = new Random();
long big = 9000000000L;
long answer = (long) (r.NextDouble() * big);

It seems to me that the total number of unique values for a Double in the range [0.0, 1.0) provides an upper-bound for the number of unique Int64 it can possibly generate. A loose upper-bound, in fact, as many different Doubles will map to the same Int64.

Hence, I would like to know: what is the total number of unique values for a double in the range [0.0, 1.0)?

Even better if you can tell me what is the largest value "big" can take so that "answer" can be a value from the range [0,big), and whether the distribution of values of "answer" is uniform, assuming that Random.NextDouble() is uniform.

Edit: Double (double) here refers to IEEE 754 floating-point double, while Int64 (long) and Int32 (int) refer to 64-bit and 32-bit signed 2's complement respectively.

---

Inspired by this question: Generating 10 digits unique random number in java

While I used C#, this question is language-agnostic and is more about discrete mathematics than programming, but it bothers me not mainly from a sense of mathematical curiousity, but from that of a programmer wanting to use a formula only if it does what it is supposed to do and from a security viewpoint.

Answer 1

IEEE-754 has 11 bits of exponent, and 52 of mantissa. Assuming the sign bit is 0 (positive), If the exponent ranges from 0x001 to 0x3FE, the value is a standard floating point number between 0 and 1. The mantissa is interpreted with a leading 1 that is not stored. For each of these 0x3FE values for the exponent, there are 2^52 values of the mantissa. In addition, if the exponent is 0x000, the mantissa is interpreted without that leading value, but as if the exponent were 0x001, for a total of 0x3FF = 1023 exponents where all mantissas are valid. This is a total of 1023*2^52 values. In addition, negative 0 may count, which is one more value.

If random doubles were generated uniformly from all values, then this would indeed produce a bias when multiplying in order to generate an Int64. However, any reasonable random library will approximate a uniform distribution on [0, 1), and this will not be biased when turning it into an Int64. The largest value for "big" that will allow all integers in [0, big) to be produced is 2^53 -- the resolution of the 2^52 numbers between 1/2 and 1 is 2^(-53). However, it's often the case that these numbers are produced by dividing random integers by the integer range (usually Int32) meaning you can't actually produce more numbers than this source. Consider directly combining two Int32s instead, e.g. by shifting one by 32 bits and combining them into an Int64. (Though be wary -- the state space for the generator might only be 32 bits.)

Answer 2

As a corollary to your question, I'll tell you that the Random C# generator uses internally a generator that "gives him" numbers between 0...Int32.MaxValue - 1. Then it divides the number by Int32.MaxValue (technically it multiplies by the inverse of that number) to return a double. So in C#, there are only Int32.MaxValue possible doubles returned (0...Int32.MaxValue - 1)

Answer 3

The IEEE754 is pretty clear on the precision of doubles:

http://en.wikipedia.org/wiki/IEEE_754-2008

You have 52 bits of precision plus an additional assumed bit.

You have exponents from -1022 to 1023, about 11 bits, including a sign.

The 64th bit is the overall sign for the number.

We'll ignore subnormalized numbers.

You're asking about exponents between -1022 and 0. This means you have about 10 of the available 11 bits of exponent available to you.

You have 52+1 bits of mantissa available.

This is about 62 bits of usable precision to represent 2**62 distinct values from

Answer 4

@wnoise pretty much nailed it, but here's my two cents.

IEEE floats can be compared and incremented as integers with some restrictions, see this question for details. So, if we cast +0.0 and 1.0 to 64 bit integers, we get the number of steps between zero and one:

#include <iostream>

int main()
{
        double zero = 0.0;
        double one = 1.0;
        unsigned long long z = *reinterpret_cast<unsigned long long*>(&zero);
        unsigned long long o = *reinterpret_cast<unsigned long long*>(&one);
        std::cout << z << std::endl;
        std::cout << o << std::endl;
}

This gives me 0 and 4607182418800017408, respectively, i.e. there are 4607182418800017408 unique double values in the range [0.0, 1.0).

Answer 5

The total number of unique values for a double in the range [0.0, 1.0) depends on the representation of double in the particular environment.

One of the most common representation is the one specified by IEEE 754. That format is e. g. mandated by Java and C# (see 1.3 Types and variables for the latter).

Answer 6

That depends on the implementation of double.There are implementations that do not allow denormalized values and leave out the leading one; determining the number of possible values here is easy:

• there are a few "special" values (0, +0, -0, +∞, -∞, silent NaN, signalling NaN) that typically cost you one possible exponent
• there is no way that shifting the mantissa and modifying the exponent gives an equivalent number

If your implementation allows denormalized values, determining this number becomes a bit more difficult, but I'd start by mapping the possible values in this representation to the equivalent representation with the fixed leading one (which will use one bit less in the mantissa); if you've found an appropriate mapping, this will be injective, and you have reduced the problem to a simpler one.