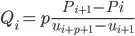I think I found the right way to re-use the de Boor's algorithm for curve derivatives.
First, we consider the definition of the B-Spline curve. It is a linear combination of control points:
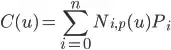 (1)
(1)
Hence, the derivative is a linear combination of the basis-function derivatives
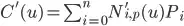 (2)
(2)
The derivative of the basis function is defined as follows:
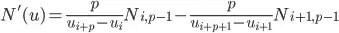 (3)
(3)
We plug-in (3) into (2) and after some algebra kung-fu, described here http://public.vrac.iastate.edu/~oliver/courses/me625/week5b.pdf, we obtain:
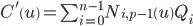 (4),
where
(4),
where 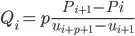
The derivative of the B-Spline curve is nothing else but a new B-Spline curve of (p-1) degree built on top of the new control points Q.
Now, to employ the de Boor's algorithm we compute the new control point set and lower the spline degree p by 1:
def deBoorDerivative(k, x, t, c, p):
"""
Evaluates S(x).
Args
----
k: index of knot interval that contains x
x: position
t: array of knot positions, needs to be padded as described above
c: array of control points
p: degree of B-spline
"""
q = [p * (c[j+k-p+1] - c[j+k-p]) / (t[j+k+1] - t[j+k-p+1]) for j in range(0, p)]
for r in range(1, p):
for j in range(p-1, r-1, -1):
right = j+1+k-r
left = j+k-(p-1)
alpha = (x - t[left]) / (t[right] - t[left])
q[j] = (1.0 - alpha) * q[j-1] + alpha * q[j]
return q[p-1]
Test:
import numpy as np
import math as m
points = np.array([[i, m.sin(i / 3.0), m.cos(i / 2)] for i in range(0, 11)])
knots = np.array([0, 0, 0, 0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 1.0, 1.0, 1.0, 1.0])
def finiteDifferenceDerivative(k, x, t, c, p):
""" Third order finite difference derivative """
f = lambda xx : deBoor(k, xx, t, c, p)
dx = 1e-7
return (- f(x + 2 * dx) \
+ 8 * f(x + dx) \
- 8 * f(x - dx) \
+ f(x - 2 * dx)) / ( 12 * dx )
print "Derivatives: "·
print "De Boor:\t", deBoorDerivative(7, 0.44, knots, points, 3)
print "Finite Difference:\t", finiteDifferenceDerivative(7, 0.44, knots, points, 3)
Output:
Derivatives:
De Boor: [10. 0.36134438 2.63969004]
Finite Difference: [9.99999999 0.36134438 2.63969004]
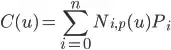 (1)
(1)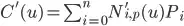 (2)
(2)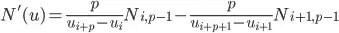 (3)
(3)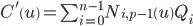 (4),
where
(4),
where