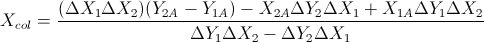How do I plot the gradient calculated from a multivariable function?

Question

Let's say I have following python code:

import numpy as np
import matplotlib.pyplot as plt

fig=plt.figure()
ax=plt.axes(projection='3d')
x=y=np.linspace(1,10,100)
X,Y=np.meshgrid(x,y)
Z=np.sin(X)**3+np.cos(Y)**3
ax.plot_surface(X,Y,Z)
plt.show()

How do I calculate from this code the gradient and plot it? I am also confused in what numpy.gradient() function exaclty returns.

I have here the graph of the function.

Answer 1

gradient is a vector. It has 2 components (in this case, since we are dealing with function ℝ²→ℝ, X,Y↦Z(X,Y)), one which is ∂Z/∂X, (also a function of X and Y), another which is ∂Z/∂Y.

So, np.gradients returns both. np.gradient(Z), called with a 100×100 array of Z, returns a list [∂Z/∂X, ∂Z/∂Y], both being also 100×100 arrays of values: a 100×100 arrays of ∂Z/∂X values, and a 100×100 arrays of ∂Z/∂Y values.

As for how to plot it, it is up to you. How would you like to plot it? You could use the gradient to alter colors, for example. Or draw arrows.

Answer 2

Here is the practical way to achieve it with Python:

import numpy as np
import matplotlib.pyplot as plt

# Some scalar function of interest:
def z(x, y):
    return np.power(np.sin(x), 3) + np.power(np.cos(y), 3)

# Grid for gradient:
xmin, xmax = -7, 7
x = y = np.linspace(xmin, xmax, 100)
X, Y = np.meshgrid(x, y)

# Compute gradient:
dZ = np.gradient(Z, x, y)

# Gradient magnitude (arrow colors): 
M = np.hypot(*dZ)

# Grid for contour:
xh = yh = np.linspace(xmin, xmax, 400)
Xh, Yh = np.meshgrid(xh, yh)

# Plotting gradient & contour:
fig, axe = plt.subplots(figsize=(12, 12))
axe.contour(Xh, Yh, Zh, 30, cmap="jet", linewidths=0.75)
axe.quiver(X, Y, dZ[1], dZ[0], M, cmap="jet", units='xy', pivot='tail', width=0.03, scale=5)
axe.set_aspect("equal")  # Don't stretch the scale
axe.grid()

It renders:

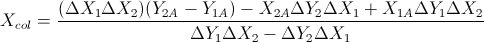
There are two visualizations of interest to see the gradient:

• Quiver which renders the vector field, see plt.quiver and advanced quiver to tune arrows;
• Contour which renders isopleth curves (levels), see plt.contour to adapt levels.

As expected gradient is orthogonal to contour curves.